Problem statement: 2 out of 5 times I run a complex Dynamo graph, the program crashes.
The probability of getting exactly k successes in n independent Bernoulli trials is given by the probability mass function:
\( P(x) = \begin{pmatrix} n\\ x \end{pmatrix} p^xq^{n-x}\\ P(x) = binomial\ probability\\ x = number\ of\ times\ for\ a\ specific\ outcome\\ n = number\ of\ trials\\ p = probability\ of\ success\ on\ a\ single\ trial\\ q = probability\ of\ failure\ on\ a\ single\ trial\\ \)
What is the probability of crashing the program twice in the next 3 runs?
\( P(X=2) = \begin{pmatrix} 3\\ 2 \end{pmatrix} 0.4^2 {(0.6)}^{3-2} = 0.288 = 28.8\% \)
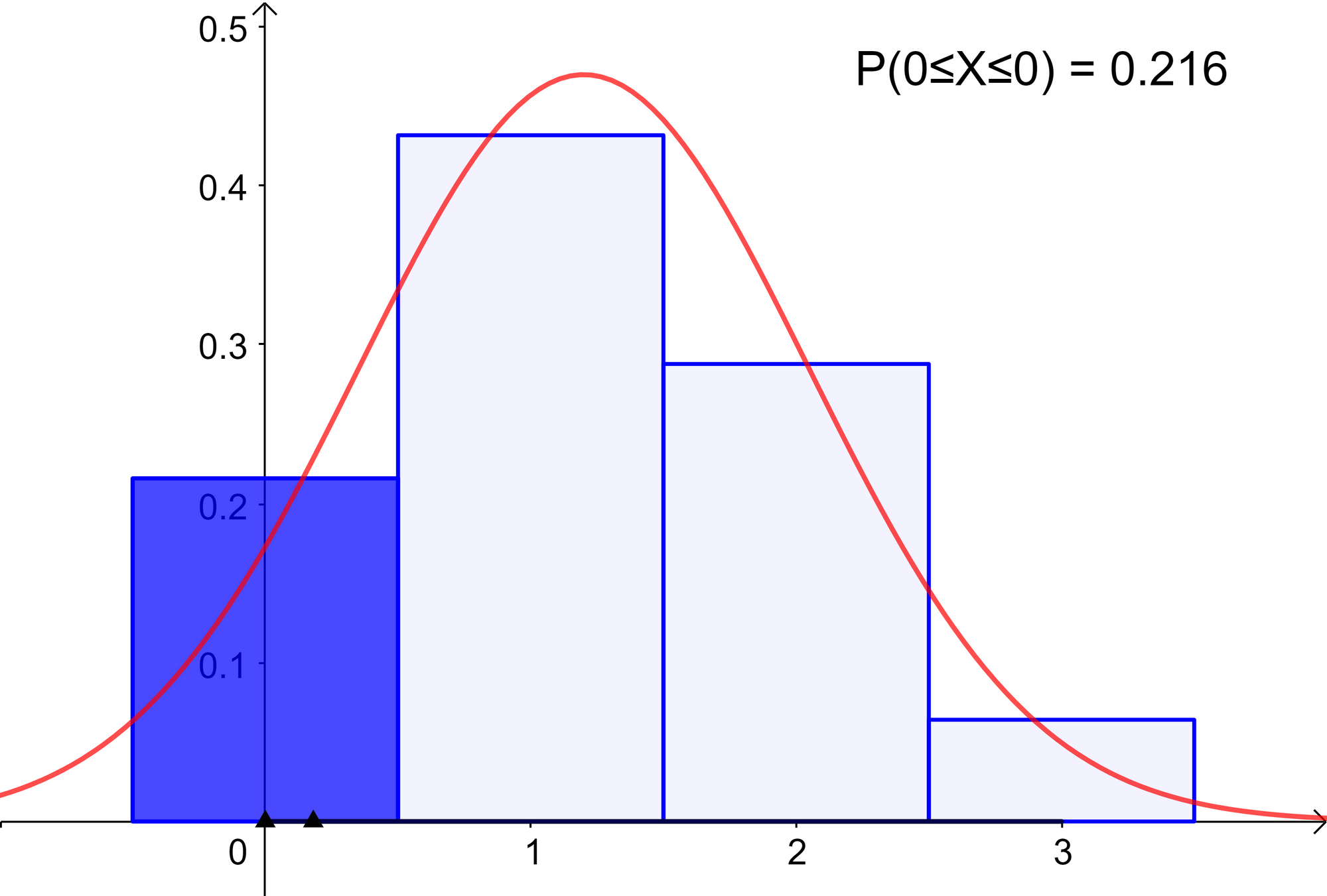
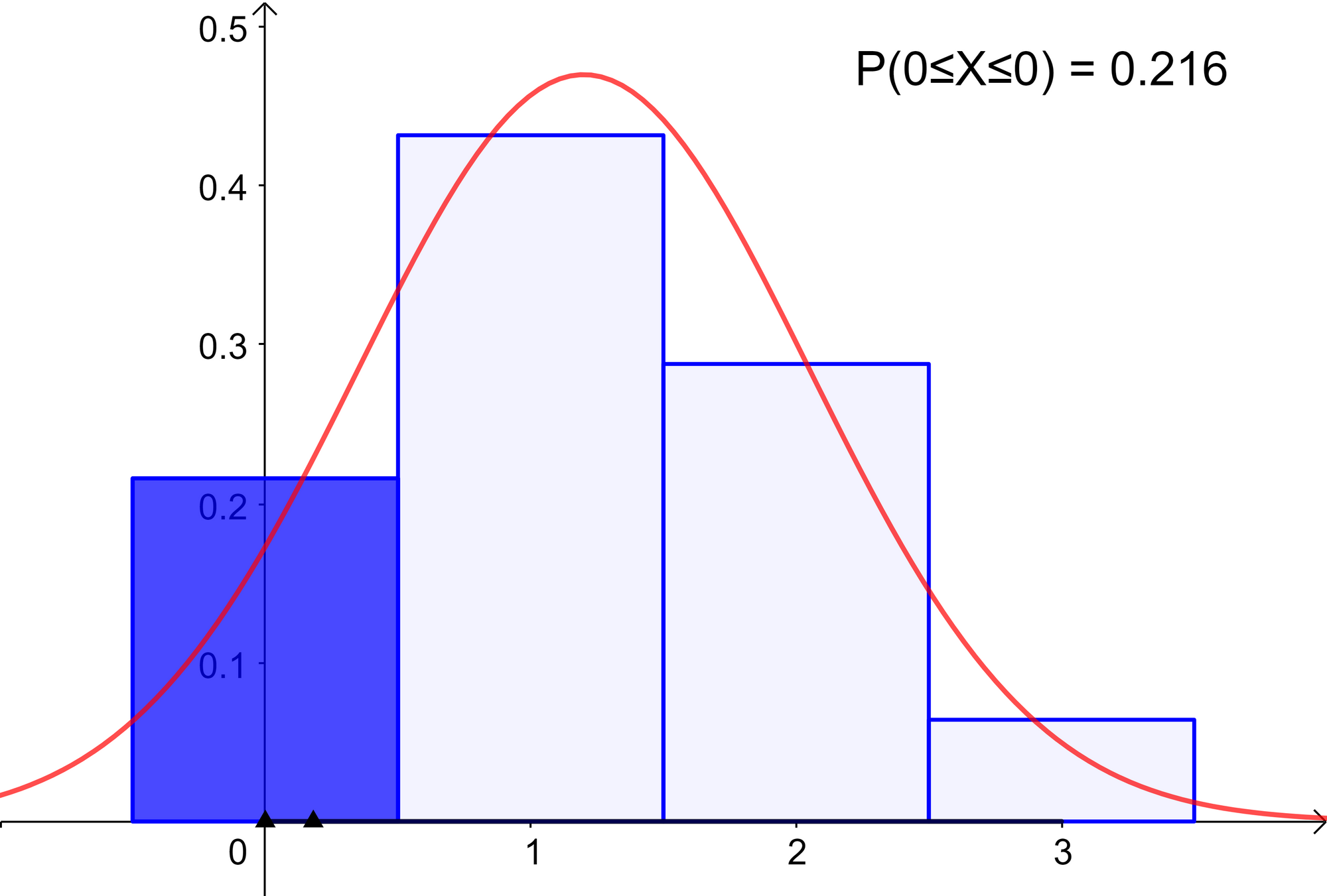
What is the probability of NOT crashing the program in the next 3 attempts?
Come on! It's not a miracle. It's definitely more than that.
\( P(X=0) = \begin{pmatrix} 3\\ 0 \end{pmatrix} 0.4^0 {(1-0.4)}^{3-0} = 0.216 = 21.6\% \)
It can also be interpreted as: probability of NOT crashing the program at any of the 3 trials
\( P(X=0) = 0.6 * 0.6 * 0.6 = 0.216 = 21.6\% \)
What is the probability of crashing the program at least once in the next 3 runs?
It could be seen as the probability of crashing the program 1, 2 OR 3 times.
\( P(X=1) = \begin{pmatrix} 3\\ 1 \end{pmatrix} 0.4^1 {(0.6)}^{3-1} = 0.432 = 43.2\% \)
\( P(X=2) = \begin{pmatrix} 3\\ 2 \end{pmatrix} 0.4^2 {(0.6)}^{3-2} = 0.288 = 28.8\% \)
\( P(X=3) = \begin{pmatrix} 3\\ 3 \end{pmatrix} 0.4^3 {(0.6)}^{3-3} = 0.064 = 6.4\% \)
And, add them up:
\( P(X\ge1) = 0.432 + 0.288 + 0.064 = 0.784 = 78.4\% \)
Also, more elegantly, it can be interpreted as: 1 minus the probability of NOT crashing the program at any of the 3 trials. Trial 1: does not crash, Trial 2: does not crash Trial 3: does not crash.
\( P(X\ge1) = 1 - (0.6 * 0.6 * 0.6) = 1 - 0.216 = 0.784 = 78.4\% \)
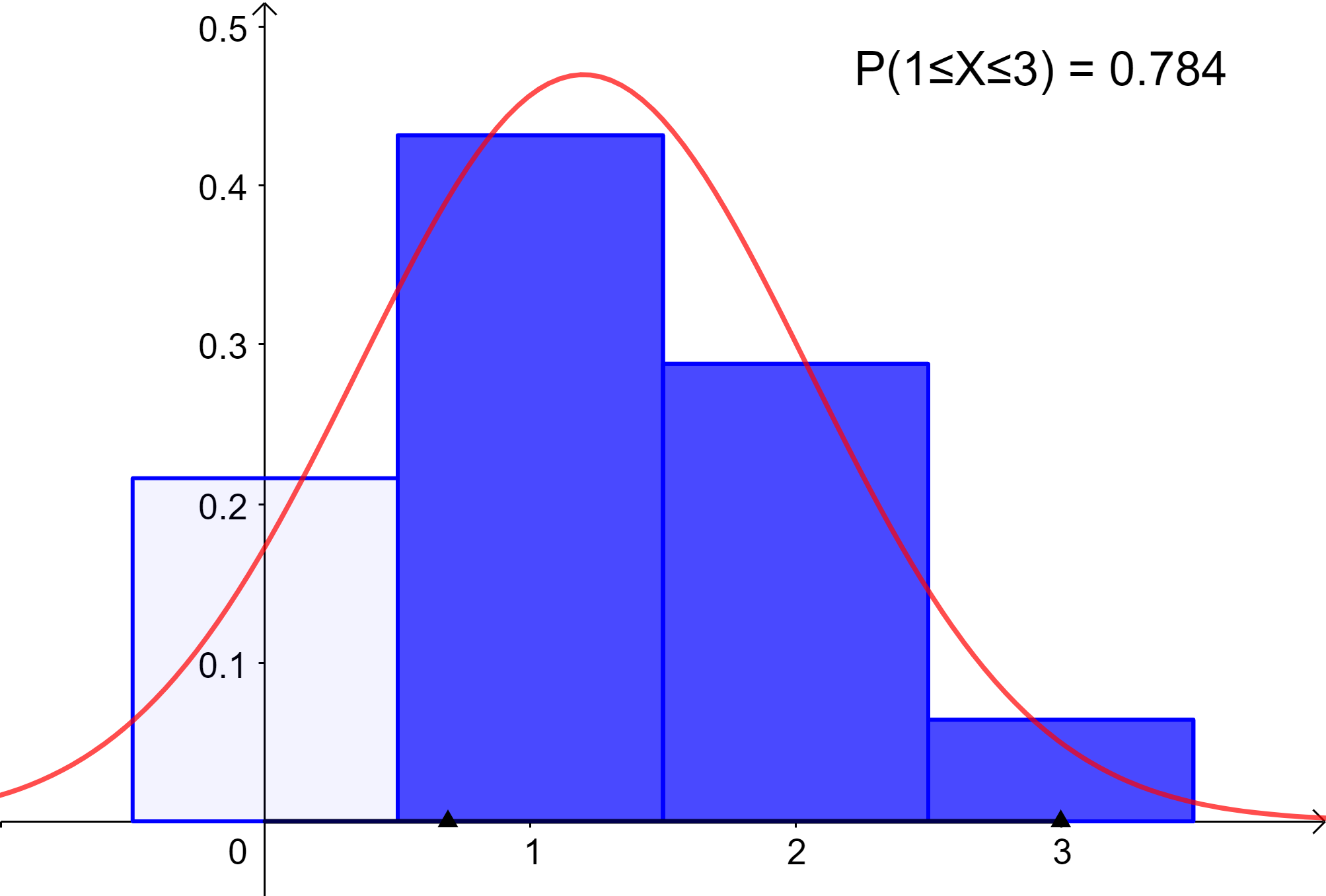
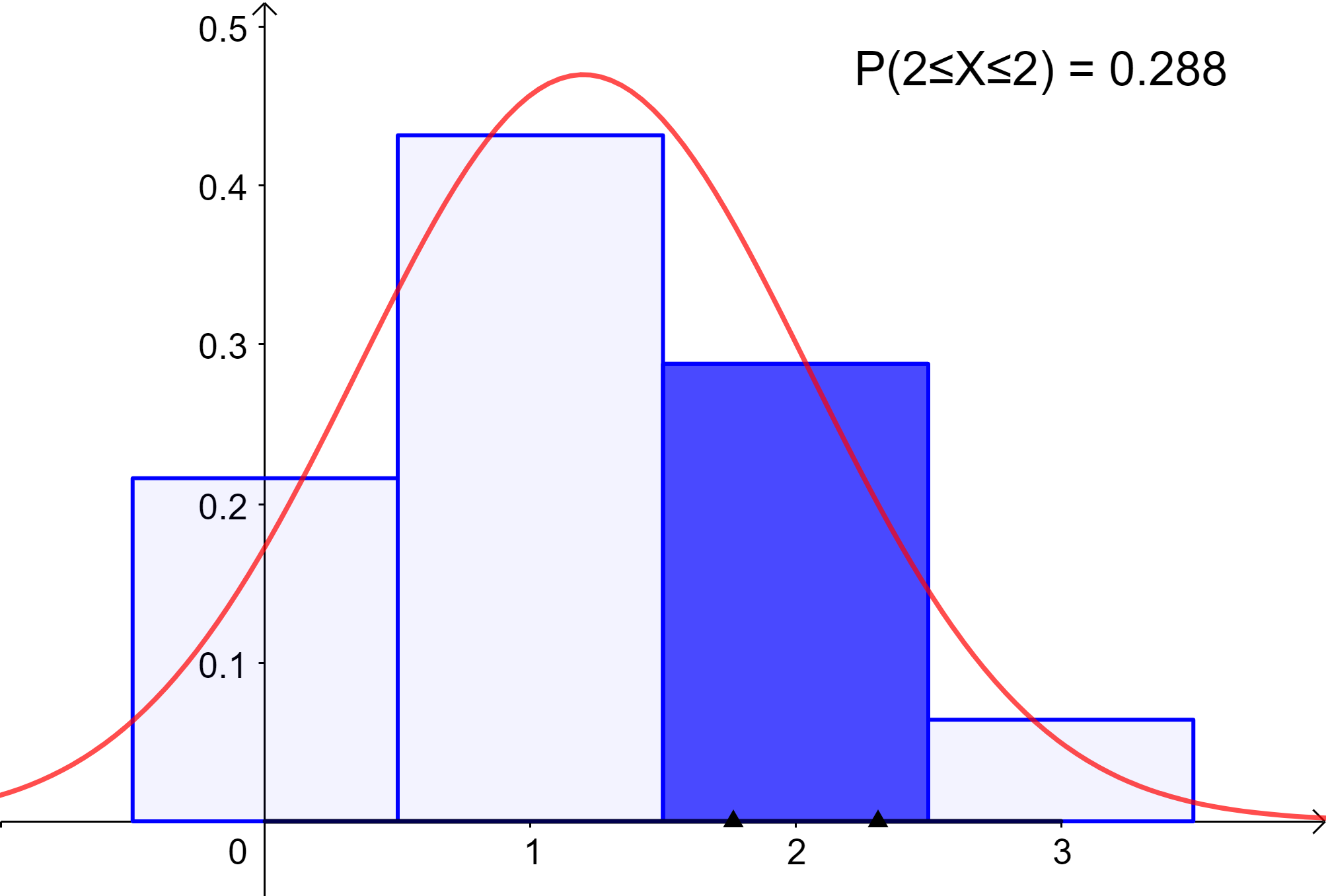
What is the probability of crashing the program at least twice in the next 3 runs?
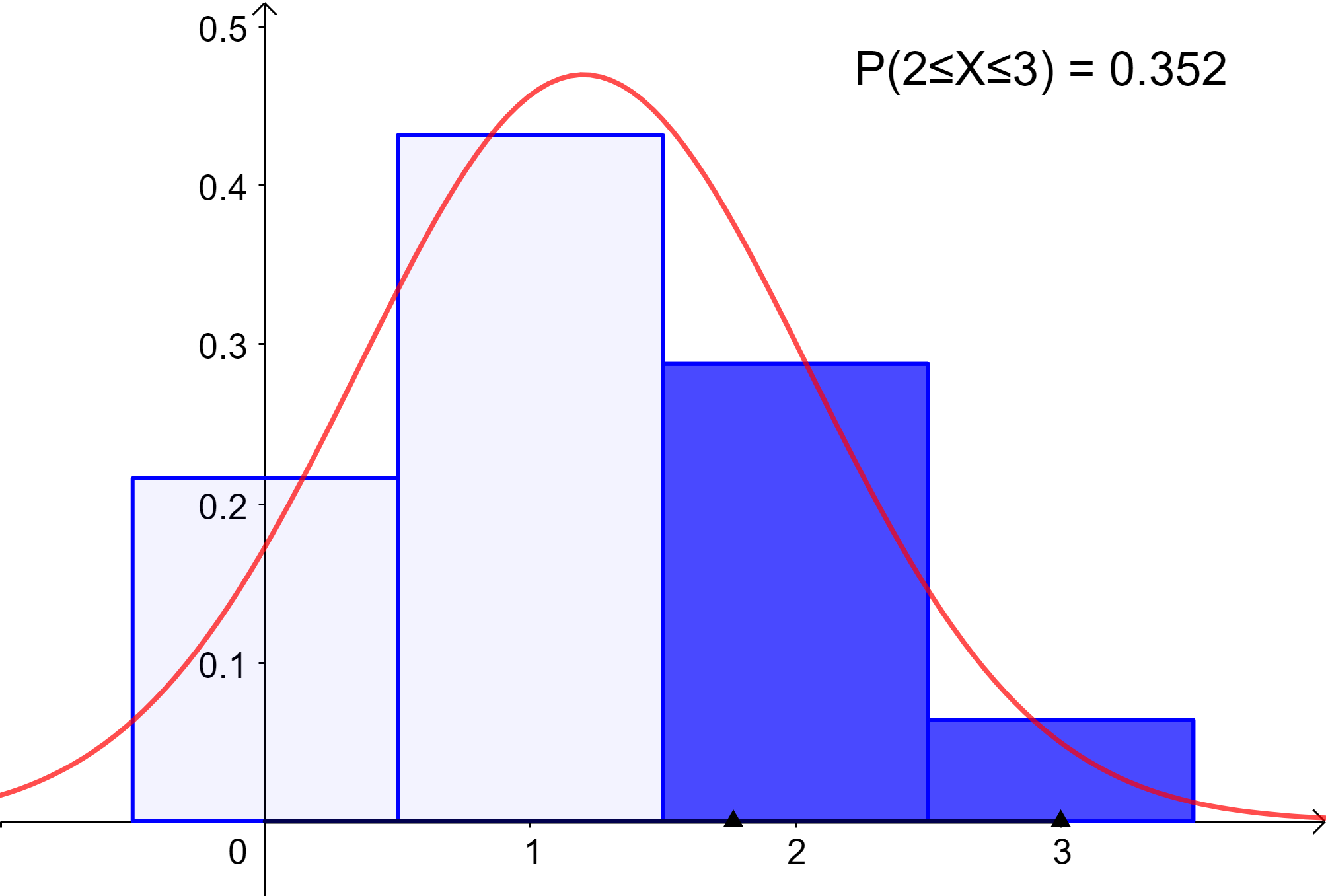
It is the probability of crashing 2 OR 3 times
\( P(X=2) = \begin{pmatrix} 3\\ 2 \end{pmatrix} 0.4^2 {(0.6)}^{3-2} = 0.288 = 28.8\% \)
\( P(X=3) = \begin{pmatrix} 3\\ 3 \end{pmatrix} 0.4^3 {(0.6)}^{3-3} = 0.064 = 6.4\% \)
Adding them up:
\( P(X\ge2) = 0.288 + 0.064 = 0.352 = 35.2\% \)
I found a very nice Binomial distribution calculator based on GeoGebra. Check the link below:
Adding KaTeX to a blog post: